Training a Perceptron on Logical Operators

  • 7/1/2024
  • 4-minute read

One of the fundamental concepts in machine learning domain is the perceptron, an algorithm inspired by the functioning of a neuron. In this blog post, we will explore the intricacies of perceptron, understand how they learn, and delve into the practical aspect of training a perceptron on logical operators.

What is a Perceptron?

A perceptron is a basic unit of a neural network, mimicking the behavior of a biological neuron. It takes inputs, processes them using a defined function, and produces an output. The key to its learning lies in adjusting weight values associated with inputs. These values encapsulate what the perceptron has learned and can be fine-tuned based on the correctness of the output.

Components of a Perceptron:

  • Inputs: The data provided to the perceptron for processing.

  • Weights: Parameters that the perceptron adjusts during training, influencing the output.

  • Bias: An independent value that can also be adjusted during training.

  • Activation Function: A function that determines whether the perceptron should “fire” based on the processed inputs.

  • Output: The result produced by the perceptron.

Training a Perceptron on Logical Operators:

Let’s take the example of training a perceptron to perform a logical OR operation. We know that the OR statement Returns True if either of the operands is true.

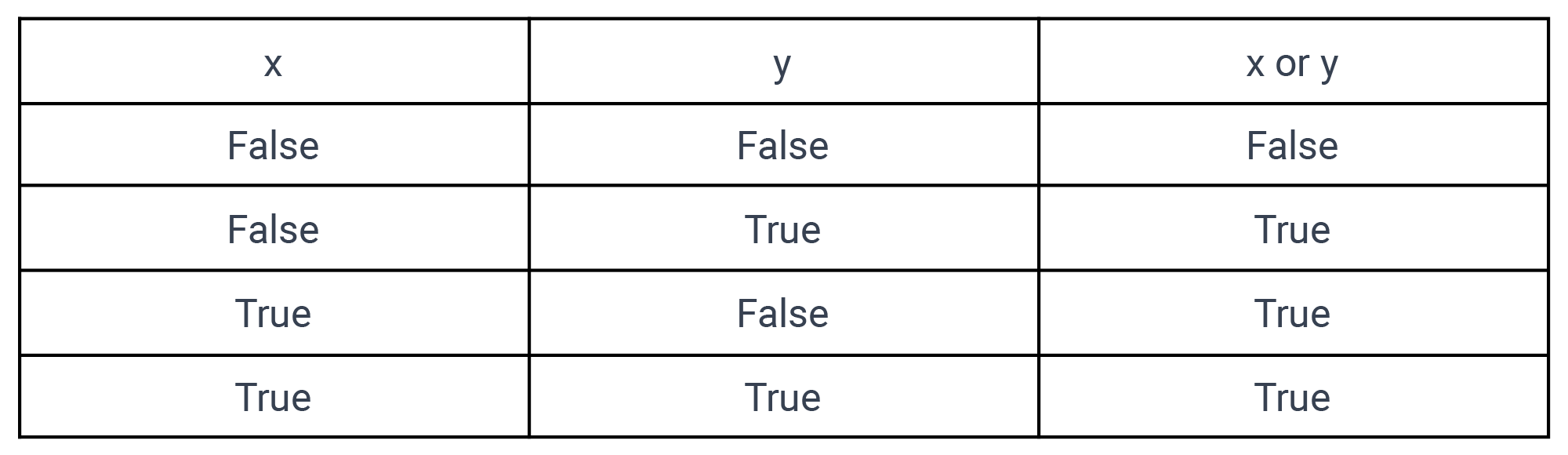
image

Logical OR Operator

  • Convert the table above into a training set, comprising input combinations and their corresponding desired outputs (0 or 1).
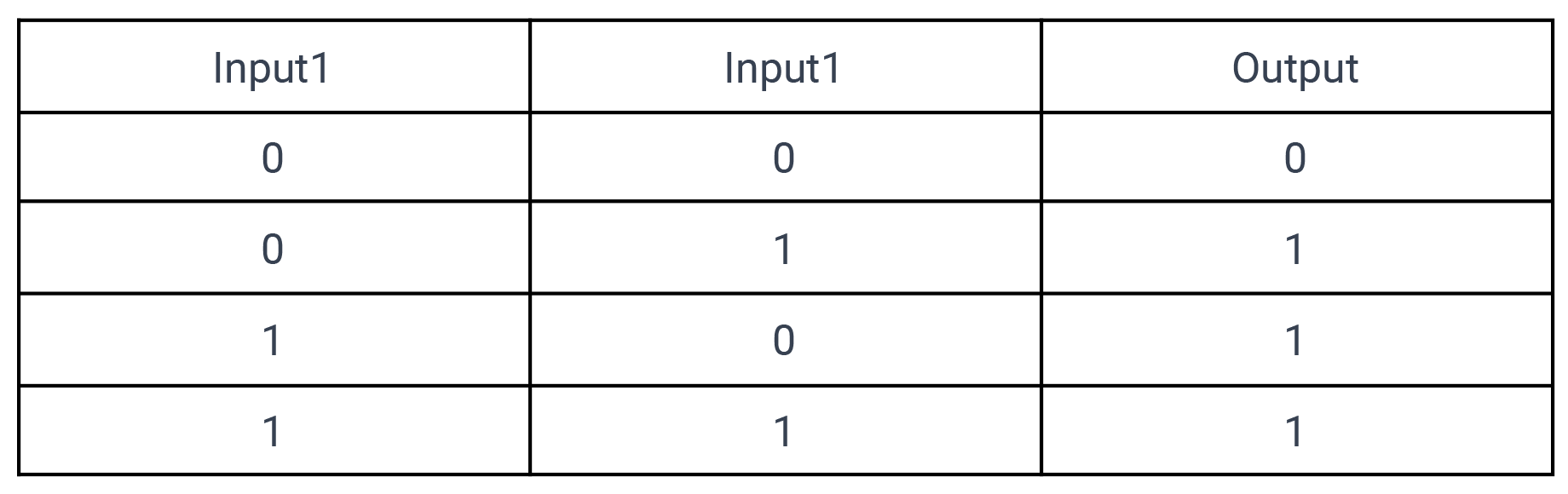
image

Training Set

  • The perceptron is initially given random weights and bias that are values between -1 & 1
image

Weights & Bias

  • For each line in the training set, the perceptron processes the inputs using the activation function.

$$ f(x) = \begin{cases} 1 &\text{if}\space \space w \space. \space x \space + \space b \space > \space 0 \newline 0 &\text{otherwise} \end{cases} $$

This simply means addition of all the inputs multiplied by their weights, plus the bias and then compare to zero

If(input1 * weight1 + input2 * weight2 + bias) > 0 then fire perceptron

  • If the output matches the desired output, no adjustments to weights are made.

  • If there’s an Error (difference between actual and desired output), weights and bias are adjusted based on the error value.

  • The process continues until the perceptron produces the correct output for all inputs. Repeating the training set through the perceptron is termed an Epoch.

Step-by-Step Weight Adjustment:

Let’s consider our basic perceptron formula:

  if(input1 * weight1 + input2 * weight2 + bias) > 0

We’ll work through a scenario where the perceptron initially makes incorrect predictions and then adapt its weights to improve accuracy.

  • Step 1: First Line Prediction

    • Given the first input (0, 0)
    input1 = 0, input2 = 0
weight1 = -0.4, weight2 = -0.8
bias = -0.4

if(0 * -0.4 + 0 * -0.8 + -0.4) > 0
=> if(-0.4) > 0
=> 0

    The prediction matches the expected output for the first line, so no adjustments to weights and bias are made.

  • Step 2: Second Line Prediction

    • Now, let’s consider the second input (0, 1)
    input1 = 0, input2 = 1
weight1 = -0.4, weight2 = -0.8
bias = -0.4

if(0 * -0.4 + 1 * -0.8 + -0.4) > 0
=> if(-1.2) > 0
=> 0

    The perceptron produces an incorrect output for the second line. This results in an Error value of 1 and prompts us to update the weights and bias.

  • Step 3: Weight and Bias Update

    • Each input then takes the error multiplies it by itself and adds it to its weight and bias.
    input1 = 0, input2 = 1
weight1 = -0.4, weight2 = -0.8
bias = -0.4
error = 1

New weight1 = 0 * 1 + (-0.4)
=> -0.4 (remains unchanged)

New weight2 = 1 * 1 + (-0.8)
=> 0.2 

New bias = -0.4 + 1 
=> 0.6

  • Step 4: Iterative Refinement

    • We repeat this process for subsequent inputs in the training set, adjusting the weights and bias based on prediction errors.
      This table was developed in Google Sheet to demonstrate the calculations.
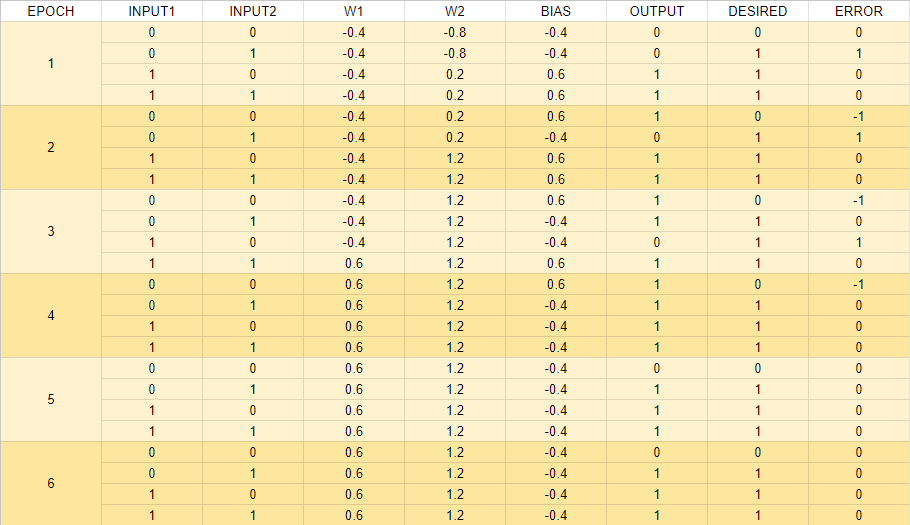
    image

    Perceptron Training

But what if you don’t want the perceptron to perform an OR operation? What if you want it to learn the AND operation instead? The key lies in changing the training set.

One of the powerful ideas driving machine learning is the ability to program a model once and retrain it multiple times to adapt to different tasks.By simply modifying the inputs and expected outputs in the training set, you can guide the perceptron to learn different logical operations.

Conclusion:

This iterative process of comparing predictions to expected outcomes, identifying errors, and updating weights and biases is fundamental to how a perceptron learns.

As we continue our journey, exploring the dynamic realm of machine learning for game development, I look forward to sharing more insights.

Additional resources:

machinelearningperceptrongamedev